

When Einstein developed his special theory of relativity, he primarily focused on its physical properties and interpretation rather than any mathematical construct. How this outstanding work helped Einstein in generalizing his theory of gravity

Sometimes, there exists more than one geodesic between two points. In flat spaces, the shortest distance between two points is a straight line which can be calculated using a distance formula while in curved spaces, straight lines are called geodesics which represents locally distance-minimizing paths.
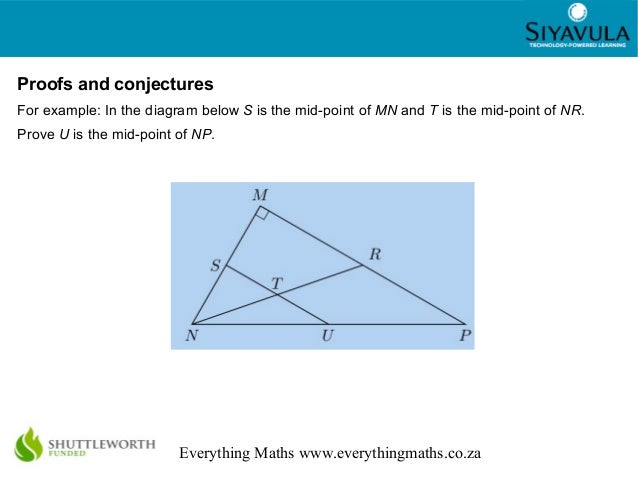
In flat spaces, the sum of all three angles of a triangle is always equal to 180° while in curved spaces the sum of triangles is either greater or less than 180° because the sides of triangles are bent outwards on a sphere and inwards on a hyperbola, see Image 1.

Because it says “ through a point not on a given line there is only one line parallel to the given line” while in curved geometry there are no parallel lines. The fifth postulate of Euclid, - the parallel postulate is completely rejected in elliptic geometry.Euclidean geometry applies to flat spaces such as a point, line, plane, etc while Riemannian Geometry is applicable to curved spaces like a cylinder, sphere, torus, etc.There was no turning back to the work of Euclid.”Ĭomparison between Euclidean and Riemannian geometry His talk was translated into several languages and created quite a sensation in mathematics. News of the lecture soon spread throughout all the centers of learning in Europe. Word spread quickly throughout Europe that Riemann had decisively broken out of the confines of Euclidean geometry that had ruled mathematics for 2 millennia. “In retrospect, this was, without question, one of the most important public lectures in the history of mathematics. Michio Kaku wrote in his book Hyperspace, Returning to the faculty meeting, he spoke with the greatest praise and rare enthusiasm to Wilhelm Weber about the depth of the thoughts that Riemann had presented.” … The lecture exceeded all his expectations and greatly surprised him. “Among Riemann’s audience, only Gauss was able to appreciate the depth of Riemann’s thoughts. Monastyrsky writes in his book Riemann, Topology, and Physics, However, Gauss was the only one who fully understood and cherished the essence of geometry which is applicable to curved surfaces. Many scientists in the audience didn’t understand the lecture because it was too ahead of its time to be grasped and appreciated by everyone. In the last part, he tried to relate his geometry to the real world. In the beginning of his lecture, he focused on defining n-dimensional space, geodesics, curvature tensors, etc. In 1854, he delivered the lecture entitled - “ On the Hypotheses Which Lie at the Foundations of Geometry”, to fulfill the Habilitation period and it was so phenomenal that it became the cornerstone for a new kind of geometry i.e Riemannian geometry. He worked for 2.5 years on his dissertation about the representability of functions by trigonometric series. In that period, he had to write an extensive dissertation and deliver a lecture. Now, to win a permanent position at the University of Göttingen, Gauss recommended Riemann for the post of Habilitation (post-doctoral qualification). Gauss expressed that Riemann was a person with “ a gloriously fertile originality” after he supervised his PhD thesis in the area of complex variables. His manner suited Riemann, who adopted it and worked according to Dirichlet’s methods." Dirichlet loved to make things clear to himself in an intuitive substrate along with this he would give acute, logical analyses of foundational questions and would avoid long computations as much as possible. “Riemann was bound to Dirichlet by the strong inner sympathy of a like mode of thought. He learned elliptic function theory from Eisenstein, whereas Dirichlet was the one who most influenced him. He also spent some of his time at Berlin University where he found brilliant mentors including Jacobi, Dirichlet, and Eisenstein. At Göttingen, he found a great teacher, Carl Friedrich Gauss (1777–1855), famous for his works in a wide range of areas in mathematics. Bernhard Riemann (1826–1866) was a German mathematician who studied and served at the University of Göttingen.


 0 kommentar(er)
0 kommentar(er)
